AC VOLTAGE RESISTOR

AC Voltage Applied to a Resistor

In this section, we will deal with an electric circuit, where an AC voltage is applied across a resistor. Let us consider the circuit shown below. We have a resistor and an AC voltage V, represented by the symbol ~, that produces a potential difference across its terminals that varies sinusoidally. Here, the potential difference or the ac voltage can be given as,

v=vmsinωt

Here, vm is the amplitude of the oscillating potential difference and the angular frequency is given by ω.

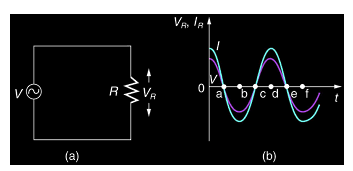
The current through the resistor due to the present voltage source can be calculated using the Kirchhoff’s loop rule, as under,

∑V(t)=0

Here, using this equation, we can write,

vmsinωt=iR

Or,

i=vmRsinωt

Here, R is the resistance of the given resistor and hence we can write,

i=imsinωt

From the Ohm’s law, we can write,

im=vmR

as it works equally well for AC voltages and DC voltages. We saw that the voltage across the resistor and the current passing through it are both sinusoidal quantities and are represented by the graph shown in the figure above. Both the quantities are in-phase with each other.

p=i2R=i2mRsin2ωt

The average value of power over the complete cycle is given as,

p¯=i2R=i2mRsin2ωt

Here the quantities im and R are constants and hence, the above equation is evaluated as,

p¯=i2mRsin2ωt

Using trigonometry, we have sin2ωt=12(1−cos2ωt), and we can write sin2ωt=12(1−cos2ωt)and since cos2ωt=0, we can write,

sin2ωt=12

Thus we can also write,

p¯=12i2mR

It is important to note that the AC power can also be expressed as DC power if we denote the current in terms of the effective current or the root mean square current.

Irms=i2¯−−√=12i2m−−−−√=im2√=0.707im

Share on Google Plus

About TECHNOLOGY IS THE WORLD

This is a short description in the author block about the author. You edit it by entering text in the "Biographical Info" field in the user admin panel.