Addition And Subtraction Of Vectors

We already learnt about the vectors and their notations in the previous physics article. Now, we will discuss vector addition and subtraction.

Vector Addition:

The vector addition is done based on the Triangle law. Let us see what triangle law of vector addition is:

Suppose there are two vectors: a→ and b→

Now, draw a line AB representing a→ with A as the tail and B as the head. Draw another line BC representing (b→) with B as the tail and C as the head. Now join the line AC with A as the tail and C as the head. The line AC represents the resultant sum of the vectors a→ and b→

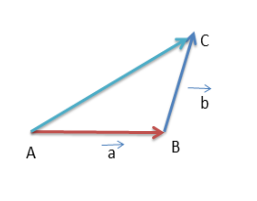
The line AC represents a→ + b→

The magnitude of a→ + b→ is:

a2 + b2 + 2ab cos θ−−−−−−−−−−−−−−−−−√

Where,

a = magnitude of vector a→

b = magnitude of vector b→

θ = angle between a→ and b→

Let the resultant make an angle of ϕ with a→, then:

tanϕ = b sin θa + b cos θ

Let us understand this by the means of an example. Suppose there are two vectors having equal magnitude A, and they make an angle θ with each other. Now, to find the magnitude and direction of the resultant, we will use the formulas mentioned above.

Let the magnitude of the resultant vector be B

Or,

B = A2 + A2 + 2AA cos θ−−−−−−−−−−−−−−−−−−−√ = 2 A cos θ2

Let’s say that the resultant vector makes an angle Ɵ with the first vector

tan ϕ = A sin θA + A cos θ = tan θ2

Ɵ = θ2

Vector Subtraction:

Subtraction of two vectors is similar to addition. Suppose a→ is to be subtracted from b→.

a→ – b→ can be said as the addition of the vectors a→ and (-b→). Thus, the formula for addition can be applied as:

a→ – b→ = a2 + b2 − 2ab cos θ−−−−−−−−−−−−−−−−−√

(-b→) is nothing but b→ reversed in direction.

Share on Google Plus

About TECHNOLOGY IS THE WORLD

This is a short description in the author block about the author. You edit it by entering text in the "Biographical Info" field in the user admin panel.